お疲れ様です、土木男です。
2次製品の側溝や境界ブロックなどの布設の際にちょっと悩ましいのが曲線部分ではないでしょうか??
フィーリングでなんとなく並べてみたけど、、、
何か違うような・・・
測点ごとのポイントは座標で落とせるけど、、
わざわざRの途中のポイントまで座標で落とすのは、
まんどくせぇ
ヽ(´Д`;)ノ
そんなとき役に立つのが
「土方カーブ」です。
土方カーブとは
単カーブ中の側点と側点の中間点のポイントを簡単な計算で求めることができます。
さらに、その中間点も簡単な計算で出すことができます。
とても便利で、現場で重宝する必殺計算技です。
では、
さっそく公式から
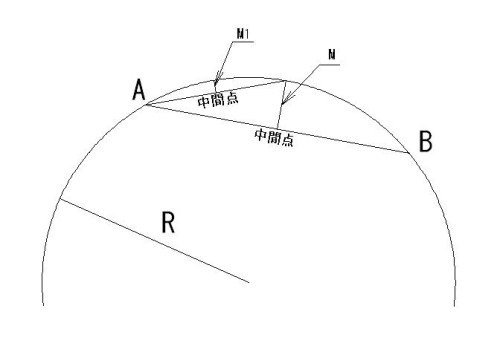
M=C×C÷8÷R
M1=M÷4
M2=M1÷4
「C」は側点Aと側点Bの直線距離です。
「R」はカーブの半径です。
「8」は定数です。
実践編
測点Aと測点Bの間をR=100の単カーブで縁石を並べたいとします。
はじめに、
『C』の距離を巻き尺等で計ります。
例えば、
巻尺の読み値が15mだっととすれば、
Mは、15×15÷8÷100となり、
M=0.281となります。
側点Aと側点Bをまっすぐに結んだ直線の中間点から垂直に0.281mの距離が
側点Aと側点BのR=100の曲線上の中間点の位置になるわけです。
現場では、測点A~測点Bまで水糸で通りを出してやって、三四五や差し金などで直角を出してやれば
簡単にポイントを出すことができます。
さらにその中間点のM1は、
M1=M÷4で求めることができ、
M1=0.281÷4=0.070となります。
さらにその中間点M1の中間点M2は、
M2=M1÷4で求めることができ、
M2=0.07÷4=0.0175となります。
これだけポイントを出してやれば、かなりキレイな曲線になります。
土方カーブはすごい便利な計算方法ですので、ぜひ覚えときましょう!!



コメント
M=C×C÷8÷R
逆にRをしり求める計算式お願いいたしますm(__)m
越伸二さん、こんにちは。
すみません、ちょっと質問の意味が分かりません。
もう少し詳しくお願いします。
R=C×C÷8M
たまに参考にさせていただいてます。
ありがとうございます。
以前、もっと正確な土方カーブの計算方法が掲載されていたような気がしたんですが、まだあるのでしょうか?
ゆうさくさん、こんにちは。
そうですね、以前はもうひとつ計算式を記載していましたが、実際の現場での施工では、水糸を張ったり巻き尺で計ったりとの作業になりますので、こちらの計算式で十分かなと思い削除しました。私の持っている参考書にも、側点間距離30m以下の場合はその誤差はほとんど問題ないとも記載されています。
CADで描いてみてもほとんど誤差がないことが分かりました!
ありがとございました。
RがわからないがMは出せるか?
出せない。
C=2m R=1mが公式にあてはまらないのはなぜですか?
玄長=半径では、ダメ?
なぜなぜくん、ご質問ありがとうございます。
ごめんなさい、私の本文には、土方カーブの公式と書いてしまってありますが、土方カーブは、公式ではなく近似式と言われる式でして、求められるのは厳密解ではなく誤差を含む近似解です。ネットによい資料があったのでリンクを貼っておきます。
http://www.ikee.jp/tech/009.pdf